Converting decimal fractions to arbitrary number systems

The problem

#include <stdio.h>

int main(void)
{
    float a = 0.1;
    float b = 0.9;

    // 1.0 - 0.1 should equal 0.9...
    if (1.0 - a == b) {
        printf("equal\n");
    } else {
        printf("not equal (?) what happened to mathematics?!\n");
    }

    printf("\nMaybe this will explain what happened\n");
    printf("a\t=\t%.20f\nb\t=\t%.20f\n1.0 - a\t=\t%.20f\n", a, b, 1.0 - a);

    return 0;
}

$ ./float 
not equal (?) what happened to mathematics?!

Maybe this will explain what happened
a   =   0.10000000149011611938
b   =   0.89999997615814208984
1.0 - a =   0.89999999850988388062

There are numerous websites that explain how IEEE-754 Floating Point numbers are stored in memory, and why we get surprising results when using numbers with a decimal point, for example in the C code above. But it’s always beneficial to have a small proof-of-concept model.

The explanation

It comes down to the fact that all numbers are stored as binary, and often it’s not possible to represent all decimal fractions with a finite number of binary digits. Just like decimal can’t represent some rational numbers with finite number of digits, eg. \[ \frac{1}{3} = 0.3333... \]

Julia code below calculates representation of decimal fractions in different bases (eg. binary, ternary, hexadecimal, base7, base64), and shows the difference between input fraction and fraction after base conversion.

function rebase_decimal(n::String, base::Int, precission::Int)::String
    fraction::Vector{Int} = fill(0, precission)
    num::Rational = parse(Int, n) // 10^length(n)
    pow::Int = idx::Int = 1

    # === The important part ===
    while num > 1 // base^precission
        if num >= 1 // base^pow
            num -= 1 // base^pow
            fraction[idx] += 1
        else
            idx += 1
            pow += 1
        end
    end
    # === End of important part ===

    @show num
    @show float(num)

    return join(fraction, " ")
end

function main()
    println("Calculating with $(ARGS[3]) digits of precission")

    r = rebase_decimal(ARGS[1], parse(Int, ARGS[2]), parse(Int, ARGS[3]))

    println("[base: 10] .$(ARGS[1])")
    println("[base: $(ARGS[2])] .$(r)")
end

main()

$ julia rebase.jl 9 2 20
Calculating with 20 digits of precission
num = 1//2621440
float(num) = 3.814697265625e-7
[base: 10] .9
[base: 2] .1 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0

$ julia rebase.jl 1 2 20
Calculating with 20 digits of precission
num = 3//5242880
float(num) = 5.7220458984375e-7
[base: 10] .1
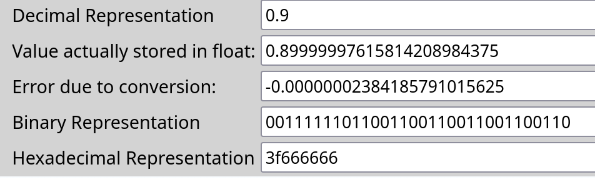
[base: 2] .0 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1

Links

Screenshot comes from here, which shows the structure of single precission floating point numbers.

Here you can verify whether my code works as advertised.